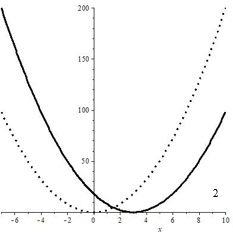
Самый наглядный способ представления информации – графический. Этот тезис применим и в математике. А при правильном подходе график может дать гораздо больше информации о поведении функции, чем просто положении точек на координатной плоскости.

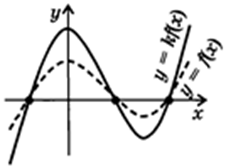
Что может рассказать график ?

1. Область определения функции – значения аргумента 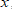, которые можно «подать на вход». Аргумент откладывается на горизонтальной оси.

2. Область значения функции – значения функции , получаемые «на выходе». Значения отмечаются на вертикальной оси.

3. Непрерывность функции. Для всех ли аргументов существуют значения?

4. Промежутки монотонности функции (возрастания или убывания).

Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции (то есть ).

Если же большему значению аргумента соответствует меньшее значение функции (то есть ), то функция называется убывающей.

Существуют функции, которые всегда возрастают (например, 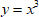) или всегда убывают (например, ).

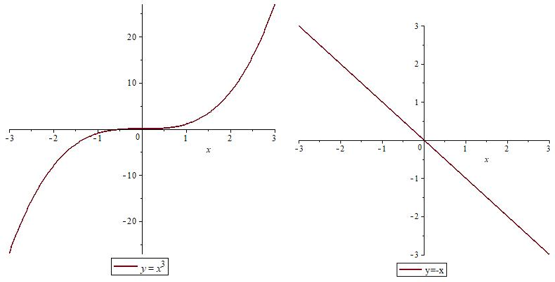
Но чаще функции имеют несколько промежутков возрастания и убывания. Например, функция убывает при и возрастает при .

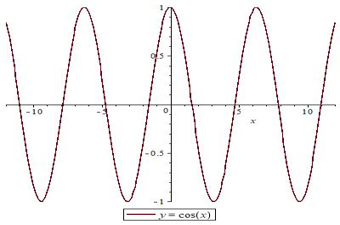
А график функции косинус имеет множество таких промежутков, сменяющих друг друга.

5. Точки минимума и максимума.

Значения аргумента, в которых функция перестает возрастать и начинает убывать, называются точками максимума. Если же в них, наоборот, функция перестает убывать и начинает возрастать – точками минимума. На графике 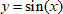красным отмечены точки минимума, синим – максимума.

Всегда возрастающие и убывающие функции таких точек не имеют.

6. Ограниченность функции. Есть ли значения, за которые функция «не заходит»?

Функции могут быть неограниченными; ограниченными сверху, снизу, слева, справа, а также сразу с нескольких сторон.

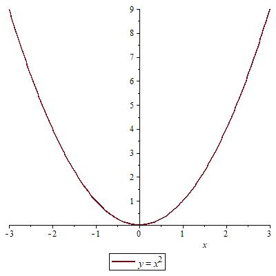
Уже знакомая нам функция косинуса, например, ограничена и сверху, и снизу. Парабола ограничена снизу. А график функции неограничен нигде.

7. Четность функции.

Функция называется четной, если выполняется равенство . Такой функцией является парабола так как верно, что . Наглядным признаком четности является симметрия графика относительно оси ОY.

Если выполняется равенство , то функция считается нечетной. Примером такого типа функций может служить кубическая парабола для которой . График нечетной функции будет симметричен относительно начала координат.

Не всякую функцию можно отнести одной из этих групп. Если не выполняется ни одно из названных условий, говорят, что функция не обладает четностью.

Рассмотрим функцию 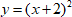и исследуем ее на четность.

Видно, что . То есть данная функция не является ни четной, ни нечетной.

8. Периодичность функции.

Если с какого-то момента график функции начинает повторяться, то такая функция называется периодичной. Таким свойством обладают все тригонометрические функции.

Помимо вышеназванных свойств у функций и их графиков есть особенные признаки, которые позволяют быстро и схематично их изобразить. Рассмотрим самые часто встречающиеся в математике зависимости.

Линейная функция

Квадратичная функция (парабола)

Кубическая парабола

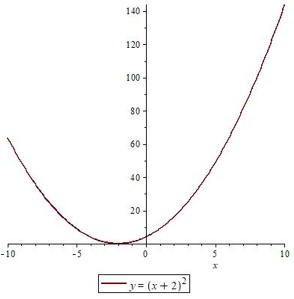
Квадратный корень

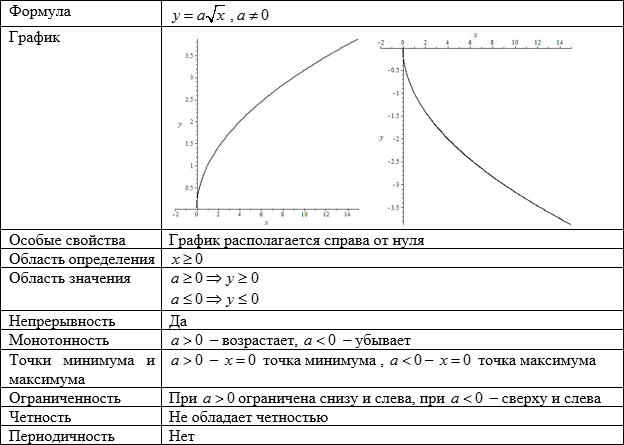
Гипербола

Окружность

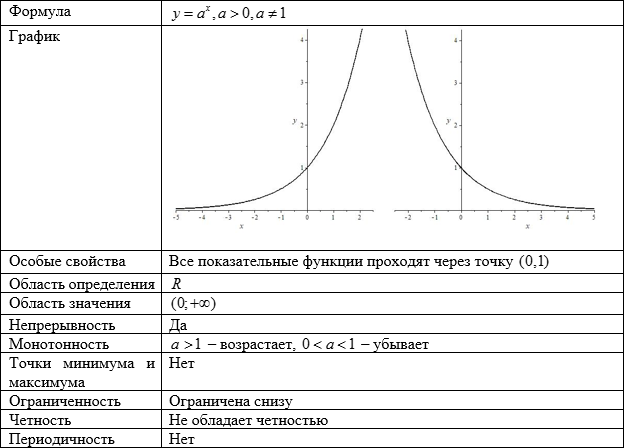
Показательная функция

Логарифмическая функция

Синус

Косинус

Тангенс

Котангенс

Преобразование графиков функции

График любой зависимости можно построить по точкам. Но в некоторых случаях гораздо проще преобразовать график какой-либо известной функции с помощью сдвигов, отражений и растяжений.

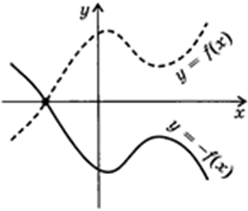
1. Симметрия относительно оси

Все абсциссы остаются неизменными, а все ординаты меняют знак на противоположный.

2. Симметрия относительно оси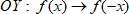

Все ординаты графика остаются неизменными, а абсциссы меняют знак на противоположный.

При таком преобразовании четной функции, график остается неизменным.

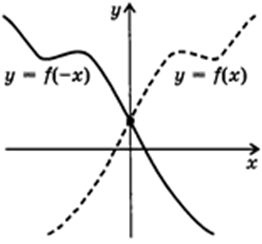
3. Сдвиг вдоль оси

Ординаты остаются неизменными, а абсциссам прибавляется . Если , то график сдвигается вправо, иначе – влево.

4. Сдвиг вдоль оси

Абсциссы не меняются, а к ординатам прибавляется . При 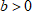график сдвигается вверх, иначе – вниз.

Обратите внимание, что в пункте 3. перед стоит знак «–», в то время как в 4. перед стоит «+». При этом знаки параметров могут быть любыми.

5. Сжатие и растяжение вдоль оси

Ординаты остаются неизменными, а абсциссы делятся на . Точки пересечения графика функции с осью остаются на месте.

6. Сжатие и растяжение вдоль оси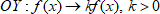

Абсциссы остаются неизменными, а ординаты умножаются на . Точки пересечения графика функции с осью остаются на месте.

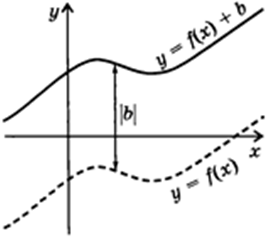
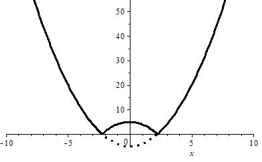
7. Модуль функции:

Точки с положительными ординатами остаются на месте, точки с отрицательными ординатами отбражаются симметрично относительно оси .

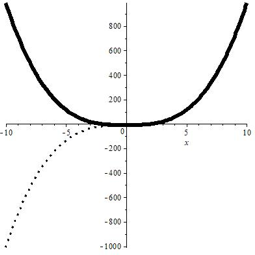
8. Модуль аргумента:

Точки, соответствующие отрицательным абсциссами, стираются. Точки с положительными абсциссами остаются на месте, а так же отображаются симметрично относительно оси . Функция становится четной.

Приведенные выше преобразования можно комбинировать и выполнять друг за другом.

Пример 1.

Построите график функции

Данный график можно получить из последовательными сжатием вдоль оси 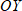в 2 раза, сдвигом вдоль оси 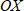на 3 вправо, сдвигом вдоль оси на 4 вверх и отражением относительно оси 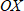.