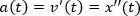ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Отсюда можно сделать несколько выводов о том, как связаны значение производной и поведение функции:
1. Функция возрастает. Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный (k > 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.
|
2. Функция убывает. Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k < 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же отрицательна.
|
3. Экстремум. Точки экстремума, отличаются тем, что в них функция и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше).
Точка максимума До неё функция возрастает, после него убывает. В точке максимума производная сменяет свой знак с плюса на минус.
Точка минимума До неё функция убывает, после него возрастает. В точке минимума производная сменяет свой знак с минуса на плюс.
|
ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ:
Допустим есть некоторая точка, которая двигается вдоль оси ОХ, и ее координата меняется со временем по закону Мы знаем определение производной: это темп изменения функции. Если говорить про темп изменения расстояния, то можно догадаться, что это скорость. То есть:
Темп изменения скорости – это ускорение. Поэтому:
Таким образом, скорость материальной точки – это первая производная от функции расстояния (координаты), а ускорение – вторая производная от функции расстояния. |
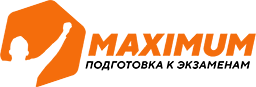

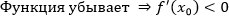
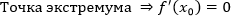


 . Получается, что
. Получается, что 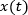 – это функция того, как меняется расстояние.
– это функция того, как меняется расстояние.