Прогрессии

Термин «прогрессия» имеет латинское происхождение («progression», что означает «движение вперед»), был введен римским математиком Боэцием в 6 веке.

Что такое прогрессия? Это тип последовательности. А что такое последовательность? Это бесконечный набор чисел, подчиняющийся определенному правилу. Например, последовательность составляют все числа, делящиеся на 2. Их бесконечно много, и они подчиняются определенному правилу. Последовательность можно задать формулой n-го члена, где n – номер члена последовательности.

Например,

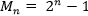(числа Мерсенна)

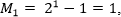
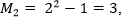
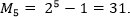
Последовательность также может задаваться правилом, по которому находят каждый ее член, если известны предыдущие. Например, первые два члена последовательности равны единице, а каждый следующий равен сумме двух непосредственно предшествующих ему. Тогда получаем последовательность чисел:

1, 1, 2, 3, 5, 8, 13, 21, … (называемых числами Фибоначчи)

Есть два вида последовательностей, которые изучаются в курсе математики– это арифметические и геометрические прогрессии.

Арифметическая прогрессия

Арифметической прогрессией называют такую числовую последовательность, каждый следующий член которой отличается от предшествующего члена на одно и то же число d.

Например, 1, 3, 5, 7…

Число d называют разностью арифметической прогрессии.

Отметим, что если d > 0, то арифметическая прогрессия является возрастающей последовательностью, если d < 0, то — убывающей последовательностью. А если d = 0 ? Это тоже прогрессия, называют ее в математике постоянной прогрессией.

Ряд натуральных чисел дает пример бесконечной арифметической прогрессии с разностью d = 1, а последовательность нечетных и четных чисел – примеры бесконечных арифметических прогрессий, у каждой из которых разность d = 2 (отличие только в первом члене прогрессии).

Если известен первый член арифметической прогрессии a₁ и ее разность d, то можно найти любой член этой последовательности по формуле:

• a_n = a₁ + d · (n?1) — формула n-го члена,

Пример: найдите члены а₈, а₁₀₀₀ арифметической прогрессии, у которой а₁ = -2, d = 5

Решение:

Найдем по записанной нами формуле:

а₈ = a₁ + d · (8 ?1) = -2 + 7 · 5 = 33.

а₁₀₀₀ = a₁ + d · (1000 ?1) = -2 + 999 · 5 = 4993.

Запишем формулы суммы n первых членов прогрессии:

Пример: определить сумму k первых нечетных чисел, начиная с единицы.

Решение:

Последовательность нечетных чисел – арифметическая прогрессия с a₁ = 1 и d = 2

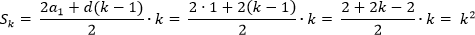
Например, сумма первых пяти нечетных чисел:

Можно убедиться, что 1 + 3 + 5 + 7 + 9 = 25.

Каждый член арифметической прогрессии равен среднему арифметическому его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену)

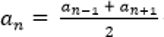• — свойство n-го члена.

Геометрическая прогрессия

Геометрической прогрессией называют такую числовую последовательность, каждый член которой, начиная со второго, равен предшествующему члену, умноженному на одно и то же (определенное для данной последовательности) число q. Число q называют знаменателем геометрической прогрессии. Предполагается, что q ? 0.

Например, 1, 3, 9, 27…

Если q > 0, то прогрессия считается знакоположительной, при q < 0 – знакопеременной.

Если |q |>1, прогрессия возрастающая, если |q | <1 – убывающая. Заметим, что при q < 0 сами члены геометрической прогрессии попеременно меняют знак и убывающей последовательности не образуют, хотя такую прогрессию все равно называют убывающей.

Если b₁ — первый член прогрессии (b₁ ? 0), а q — знаменатель прогрессии (q ? 0), то справедливы следующие формулы:

• b_n = b_{1 ·} q ^{n -1} формула n-го члена

Пример: найдите b₄, b₁₁ геометрической прогрессии, если b₁ = 3, q = 2

Решение:

По формуле найдем:

b₄ = b_{1 ·} q ^{4 - 1}= 3 · 2 ³ = 24,

b₁₁ = b_{1 ·} q ^{11 - 1}= 3 · 2 ¹⁰ = 3072.

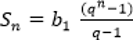• — формула суммы n первых членов;

Пример: найдите сумму пяти членов геометрической прогрессии, у которой b₁ = 2, q = 3

Решение:

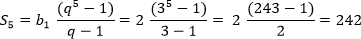
Каждый член знакоположительной геометрической прогрессии представляет собой среднее геометрическое его соседних членов (исключение составляют первый и последний члены, т.к. у них только по одному соседнему члену):

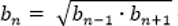• - свойство n-го члена.

Если | q | < 1, то имеем бесконечную убывающую геометрическую прогрессию, сумму которой находят по формуле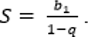

Замечание:

Формула n-го члена прогрессии:

• арифметической:a_n = a₁ + d · (n ? 1)
• геометрической: b_n = b_{1 ·} q ^{n - 1}

Зная одну формулу, легко можно получить другую – надо лишь сложение заменить умножением и умножение заменить возведением в степень, и из формулы для арифметической прогрессии получится формула для геометрической прогрессии.

Сложные проценты

Есть два вида процентов доходности – простые и сложные.

Чтобы с ними разобраться, представим двух братьев: Расчетливого Сашу и Простака Петю. Их отец дал каждому по 1000 рублей, и оба кладут их в банк. Расчетливый Саша всегда пользуется счетом со сложными процентами, а Простак Петя больше любит поступать по старинке и предпочитает счета с простыми процентами.

Сложный процент - это проценты с процентов.

У простого процента такой особенности нет, его рассчитывают от стартовой суммы, которую называют «основным капиталом». Пете легко в этом разобраться: основной капитал зарабатывает каждый год одну и ту же сумму.

Если вы откладываете деньги, занимаете их, пользуетесь кредитной картой, берёте в ипотеку или покупаете пожизненную ренту, формула сложного процента работает на (или против) вас.

Давайте выведем формулу сложных процентов. Допустим, у нас есть некоторая сумма S, в конце года мы ее увеличиваем на некоторый процент (%). Полученную сумму S₁ после начисления процентов можно посчитать так:

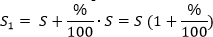
В следующем году полученную сумму снова увеличим на тот же процент. Тогда можем записать верное равенство:

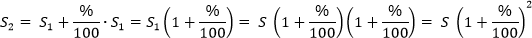
Аналогично мы можем посчитать полученную сумму еще через год:

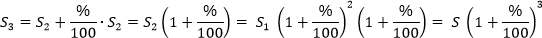
Таким образом, если периодов n, то можем записать формулу вычисления сложных процентов:

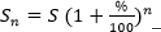начисление процентов (%) на сумму S через n периодов.

Тогда последовательность остатков долга будет следующей:

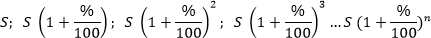
Видим, что это геометрическая прогрессия.

Итак, Саша размещает свои 1000 рублей на счете и получает ежегодно 7% дохода. Давайте посчитаем, сколько он получит за три года? В данном случае S = 1000, % = 7, n = 3, 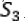– общая сумма, получаемая по формуле сложного процента:

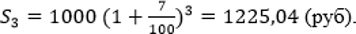
Счет Пети – тоже 7%-ный, но процент у него простой. Какие деньги заработает за три года Петя? В первый год он получит 70 рублей, столько же – во второй и в третий. Таким образом, проценты составят 3 · 70 = 210 рублей, итого общая сумма на счете - 1210 рублей. Инвестиционное решение Саши, очевидно, выгоднее.